R: Fitting frailty models with clustered, multi-event and...

frailtyMM {frailtyMMpen}

R Documentation

Fitting frailty models with clustered, multi-event and recurrent data using MM algorithm

Description

This formula is used to fit the non-penalized regression. 3 types of the models can be fitted, shared frailty model where hazard rate of j^{th} object in i^{th} cluster is

\lambda_{ij}(t|\omega_i) = \lambda_0(t) \omega_i \exp(\boldsymbol{\beta}' \mathbf{X_{ij}}).

The multi-event frailty model with different baseline hazard of different event and the hazard rate of j^{th} event for individual i^{th} is

\lambda_{ij}(t|\omega_i) = \lambda_{0j}(t) \omega_i \exp(\boldsymbol{\beta}' \mathbf{X_{ij}}).

The recurrent event model where the j^{th} event of individual i has observed feature \mathbf{X_{ij}},

\lambda_{ij}(t|\omega_i) = \lambda_0(t) \omega_i \exp(\boldsymbol{\beta}' \mathbf{X_{ij}}).

For the clustered type of data, we further assume that cluster i has n_i with j=1,...,n_{i} number of objects where they share the common frailty parameter \omega_i. For simplicity, we let \boldsymbol{\alpha} be the collection of all parameters and baseline hazard function. Then, the marginal likelihood is as follows,

Given the objective functions above, we take the clustered data as an example to illustrate the application of MM algorithm in optimizing the observed likelihood function, the observed log-likelihood function is,

where,

In order to formulate the iterative algorithm to optimize the observed log likelihood, we further define density function g_i(\cdot) based on the estimates of the parameters in k^{th} iteration \boldsymbol{\alpha}^{(k)}

Then, we construct the surrogate function to minimize the mariginal log-likelihood using the Jensen's inequality,

which successfully separated \boldsymbol{\alpha} into \boldsymbol{\theta} and (\boldsymbol{\beta}, \Lambda_{0}) where,

and let ,

And then we estimate \Lambda_{0} by,

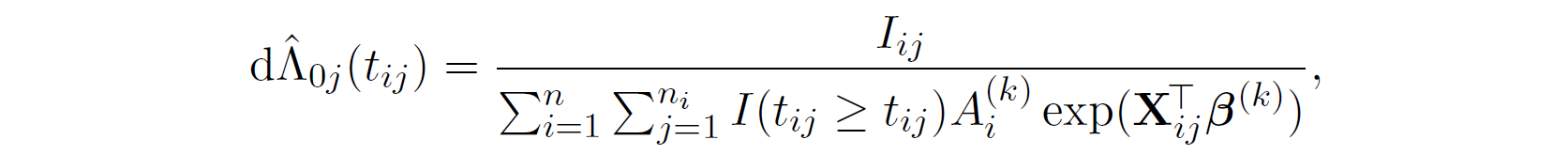
Then, we have,

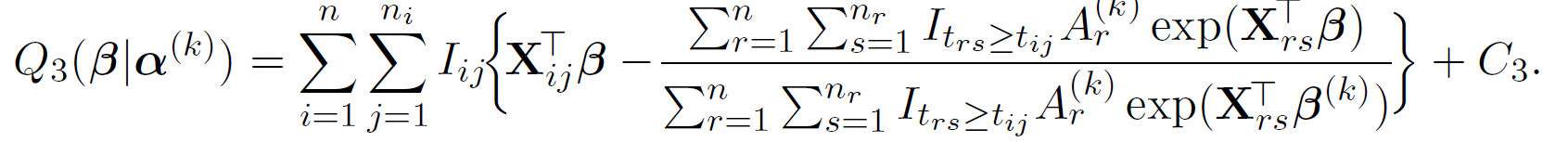
Further more, we apply hyperplane inequality to construct surrogate function for \boldsymbol{\beta} where we can update the its estimates coordinate wise,

By applying Jensen's inequality,

Finally,

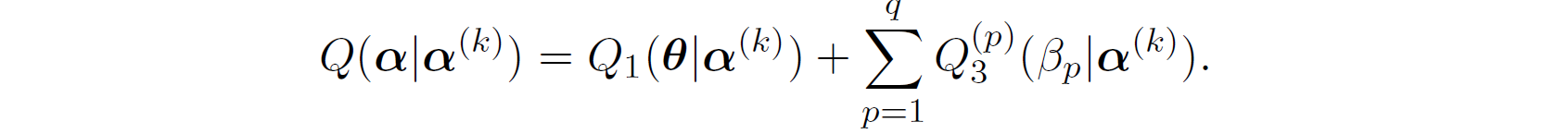
Usage

frailtyMM(
  formula,
  data,
  frailty = "gamma",
  power = NULL,
  tol = 1e-05,
  maxit = 200,
  ...
)

Arguments

`formula`	Formula where the left hand side is an object of the type `Surv` and the right hand side contains the variables and additional specifications. `+cluster()` function specify the group id for clustered data or individual id for recurrent data. `+event()` function specify the event id for multi-event data (only two events are allowed).
`data`	The `data.frame` where the formula argument can be evaluated.
`frailty`	The frailty used for model fitting. The default is "lognormal", other choices are "invgauss", "gamma" and "pvf". (Note that the computation time for PVF family will be slow due to the non-explicit expression of likelihood function)
`power`	The power used if PVF frailty is applied.
`tol`	The tolerance level for convergence.
`maxit`	Maximum iterations for MM algorithm.
`...`	additional arguments pass to the function.

Details

To run the shared frailty model, Surv(tstop, status) formula should be applied along with +cluster() to specify the corresponding clusters, if you want to run the simple frailty model without shared frailty, you do not need to use +cluster() and the formula only contains the name of the covariates. To run the multi-event model, Surv(tstop, status) formula should be applied along with +event() to specify the corresponding events. If multi-event data is fitted, please use 1,2...,K to denote the event id from the input data. To run the recurrent event model, Surv(tstart, tstop, status) formula should be applied along with +cluster() where the cluster here denotes the individual id and each individual may have many observed events at different time points.

The default frailty will be log-normal frailty, in order to fit other frailty models, simply set parameter frailty as "InvGauss", "Gamma" or "PVF", the parameter power is only used when frailty=PVF and since the likelihood of PVF (tweedie) distribution is approximated using Tweedie function from package mgcv, 1<power<2.

Value

An object of class fmm that contains the following fields:

`coef`	coefficient estimated from a specific model.
`est.tht`	frailty parameter estimated from a specific model.
`lambda`	frailty for each observation estimated from a specific model.
`likelihood`	The observed log-likelihood given estimated parameters.
`input`	The input data re-ordered by cluster id. `y` is the event time, `X` is covariate matrix and `d` is the status while 0 indicates censoring.
`frailty`	frailty used for model fitting.
`power`	power used for model fitting is PVF frailty is applied.
`iter`	total number of iterations.
`convergence`	convergence threshold.
`formula`	formula applied as input.
`coefname`	name of each coefficient from input.
`id`	id for individuals or clusters, 1,2...,a. Note that, since the original id may not be the sequence starting from 1, this output id may not be identical to the original id. Also, the order of id is corresponding to the returned `input`.
`N`	total number of observations.
`a`	total number of individuals or clusters.
`datatype`	model used for fitting.

References

Huang, X., Xu, J. and Zhou, Y. (2022). Profile and Non-Profile MM Modeling of Cluster Failure Time and Analysis of ADNI Data. Mathematics, 10(4), 538.
Huang, X., Xu, J. and Zhou, Y. (2023). Efficient algorithms for survival data with multiple outcomes using the frailty model. Statistical Methods in Medical Research, 32(1), 118-132.

Examples


# Kidney data fitted by Clustered Inverse Gaussian Frailty Model


InvG_real_cl = frailtyMM(Surv(time, status) ~ age + sex + cluster(id),
                         kidney, frailty = "invgauss")
InvG_real_cl

# Cgd data fitted by Recurrent Log-Normal Frailty Model

logN_real_re = frailtyMM(Surv(tstart, tstop, status) ~ sex + treat + cluster(id),
                         cgd, frailty = "gamma")
logN_real_re


# Simulated data example

data(simdataCL)

# Parameter estimation under different model structure and frailties

# Clustered Gamma Frailty Model
gam_cl = frailtyMM(Surv(time, status) ~ . + cluster(id), 
                   simdataCL, frailty = "gamma")


# Clustered Log-Normal Frailty Model
logn_cl = frailtyMM(Surv(time, status) ~ . + cluster(id), 
                    simdataCL, frailty = "lognormal")

# Clustered Inverse Gaussian Frailty Model
invg_cl = frailtyMM(Surv(time, status) ~ . + cluster(id), 
                    simdataCL, frailty = "invgauss")
                   
data(simdataME)

# Multi-event Gamma Frailty Model
gam_me = frailtyMM(Surv(time, status) ~ . + cluster(id), 
                   simdataCL, frailty = "gamma")


# Multi-event Log-Normal Frailty Model
logn_me = frailtyMM(Surv(time, status) ~ . + event(id), 
                    simdataME, frailty = "lognormal")

# Multi-event Inverse Gaussian Frailty Model
invg_me = frailtyMM(Surv(time, status) ~ . + event(id),
                    simdataME, frailty = "invgauss")

data(simdataRE)

# Recurrent event Gamma Frailty Model
gam_re = frailtyMM(Surv(start, end, status) ~ . + cluster(id),
                   simdataRE, frailty = "gamma")

# Recurrent event Log-Normal Frailty Model
logn_re = frailtyMM(Surv(start, end, status) ~ . + cluster(id),
                   simdataRE, frailty = "lognormal")

# Recurrent event Inverse Gaussian Frailty Model
invg_re = frailtyMM(Surv(start, end, status) ~ . + cluster(id), 
                    simdataRE, frailty = "invgauss")


# Obtain the summary statistics under fitted model

coef(gam_cl)
summary(gam_cl)

[Package frailtyMMpen version 1.2.1 Index]